title	author	cover	sticky	katex	toc	swiper_index	categories	tags	abbrlink	date	description
《白话机器学习的数学》笔记	Achuan-2	false	false	true	true	false	编程	机器学习	cd97	2021-12-18 03:01:50 -0800	本书通过正在学习机器学习的程序员绫乃和她朋友美绪的对话，结合回归和分类的具体问题，逐步讲解了机器学习中实用的数学基础知识。其中，重点讲解了容易成为学习绊脚石的数学公式和符号。同时，还通过实际的Python 编程讲解了数学公式的应用，进而加深读者对相关数学知识的理解。

0 简介

豆瓣页面：白话机器学习的数学 (豆瓣) (douban.com)

本书通过正在学习机器学习的程序员绫乃和她朋友美绪的对话，结合回归和分类的具体问题，逐步讲解了机器学习中实用的数学基础知识。其中，重点讲解了容易成为学习绊脚石的数学公式和符号。同时，还通过实际的 Python 编程讲解了数学公式的应用，进而加深读者对相关数学知识的理解。

我的机器学习第一本书。

虽然书名有一个数学，但是其实这本书讲的真的是深入浅出，不需要多高的数学基础，没有头疼看不懂的数学公式，只要学过大一的微积分，完全能看懂这本书的数学推导，无压力。写的真的好！

这本书真的让我知道什么是梯度下降算法，为什么深度学习里会有 epoch 和 batch。对机器学习和深度学习的理解突然就上了另一个台阶。

不过呢，咱也不是搞数学的，之所以看这本书只是为了更好理解机器学习而已，所以对于机器学习数学的理解，我觉得暂时可以先止步于这本书提到的，没必要深究。借助对机器学习新的理解，重要的还是先拿学到的去实践整活哈，尝试能不能举一反三来理解其他机器学习算法！

下面是我对各章的概括

第 1 章 开始二人之旅

将简要地介绍为什么机器学习越来越受人们的关注，以及使用机器学习能够做什么事情。此外，也会简单地讲解回归、分类、聚类等算法。

什么是机器学习？计算机特别擅长处理重复的任务，计算机能够比人类更高效地读取大量的数据、学习数据的特征并从中找出数据的模式。这样的任务也被称为机器学习或者模式识别，以前人们就有用计算机处理这种任务的想法，并为此进行了大量的研究，也开发了很多代码。现在我们能感觉到生活已经离不开机器学习和人工智能了，无论是人脸识别、语音识别、输入法联想、个性化广告推荐等等。

机器学习是怎么学习的呢？简单来说，为任务设计一个目标函数来量化目标，目标就是比如让回归误差最小，让分类精度最高。然后设计一个函数，根据目标函数的值不断更新函数的参数让目标函数的值符合我们的接受范围，也就是像人一样认知、学习纠错，努力让机器根据输入的数据来预测结果。

机器学习的传统任务有

• 回归（regression）：简单易懂地说，回归就是在处理连续数据如时间序列数据时使用的技术。本书以广告费和点击率的关系为例来讲解回归，介绍最小二乘法，以及梯度下降原理。梯度下降即机器学习中更新参数的方法。
• 分类（classification）：比如垃圾邮件的分类，本书以图片横纵的分类为例来讲解，介绍感知机和逻辑回归两种算法，并讲解似然函数的意义。
• 聚类（Clustering）：就是事先给你一堆数据，你并不知道每个样本的情况，让机器学习并把相似的归在一起。比如给你一堆水果，假设你不知道水果的名字，直接从外观上按水果的性质来聚类。而分类是学习的时候告诉你这些是什么水果，然后再拿一个水果考你。

使用有标签的数据进行的学习称为有监督学习，与之相反，使用没有标签的数据进行的学习称为无监督学习。从上面的介绍，我们知道回归和分类是有监督学习，而聚类是无监督学习。

第 2 章 学习回归——基于广告费预测点击量

以“根据投入的广告费来预测点击量”为题材，学习回归。我们先利用简单的例子来思考为了预测需要引入什么样的表达式，然后考虑如何才能使它接近最适合的结果。

目标函数：$E(\theta) =\frac{1}{2} \sum_{i = 1} ^ {n}\left(y_{i}-f_{\theta}\left(x_{i}\right)\right) ^ {2}$

设计一次函数来拟合：$f_{\theta}(x) =\theta_{0} +\theta_{1} x$

其梯度下降的参数更新表达式

$$ \begin{aligned} &\theta_{0}:=\theta_{0}-\eta \sum_{i=1}^{n}\left(f_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \\ &\theta_{1}:=\theta_{1}-\eta \sum_{i=1}^{n}\left(f_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x^{(i)} \end{aligned} $$

如果是多项式函数来拟合，其实也差不多

$$ f_{\theta}(x)=\theta_{0}+\theta_{1} x+\theta_{2} x^{2} \\ \theta_{j}:=\theta_{j}-\eta \sum_{i=1}^{n}\left(f_{\theta}\left(\boldsymbol{x}^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} $$

如果是多变量的函数来拟合。

$$ f_{\theta}(x) =\theta ^ {\mathrm{T}} x=\theta_{0} x_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n} $$

$$ \theta_{j} :=\theta_{j} -\eta \sum_{i = 1} ^ {n}\left(f_{\theta}\left(\boldsymbol{x} ^ {(i)}\right)-y ^ {(i)}\right) x_{j} ^ {(i)} $$

记忆公式方面：可以看到三类函数的梯度下降参数更新表达式都一样，可以把 $f_{\theta}(x^{(i)})-y^{(i)}$ 看成预测值与实际值的误差，误差为正，曲线太高，说明要往下调，误差为负，曲线太低，说明要往下调；乘以 $x_{j} ^ {(i)}$ 看作是为了避免 $x_{j} ^ {(i)}$ 为负的情况，因为就比如对于一次函数来说，在 x 轴的负半轴，误差为正，其实是 x 轴的正半轴误差为负，所以需要调和下。 （这部分的理解来自 Ele 实验室的小白也能听懂的人工智能原理，一开始并没有直接讲梯度下降，而是介绍了 Rosemblatt 感知器模型）

理解梯度下降：为了让目标函数最小，就需要找到目标函数的极小值点。如何找到呢？一种方法是直接暴力求解即正规方程，一种就是梯度下降，每次代入数据进去，看看其梯度是正还是负，然后沿着梯度的反向更新参数就好了。为什么是反向呢，就好比下山，类比下就知道，反向沿着梯度才是去山底，正向就是去山顶了。

书里还介绍了批量梯度下降，随机梯度，minibatch 随机梯度。简单说批量梯度下降就是一次迭代要求完所有数据的误差来梯度下降，问题是数据量大时，很耗时，而且如果目标函数设计的很复杂，可能会陷入局部最优，在一个山谷就卡住下不来山了；随机梯度下降就是随机抽一个数据就进行一次梯度下降了，就算陷入局部最优，又可能能跳出来，问题是由于是随机，能在全局最优点附近徘徊，精度可能不够；mini-batch 处于中间，随机抽一批来梯度下降，即能较快下降又能一定程度避免陷入局部最优值，是目前深度学习最常使用的梯度下降方法。

第 3 章 学习分类——基于图像大小进行分类

以“根据图像的大小，将其分类为纵向图像和横向图像”为题材，学习分类。与第 2 章一样，我们首先考虑为了实现分类需要引入什么样的表达式，然后考虑如何才能使它接近最适合的结果。

讲了感知机和逻辑回归。

3.1 感知机

感知机可以看成是一个简单的神经元。

数据标签：把标签设置为 1 和-1

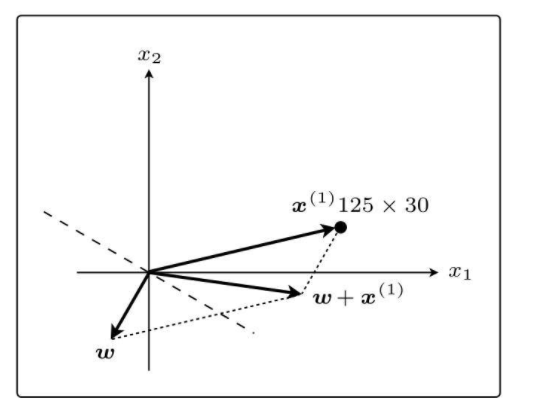
学习过程：先随机生成一个权重向量，然后进行预测：如果正确分类，就不更新 $w$；如果错误分类，就更新 w，通过向量的加法或减法，调整向量的方向，使其接近正确方向。

$$ \boldsymbol{w}:= \begin{cases}\boldsymbol{w}+y^{(i)} \boldsymbol{x}^{(i)} & \left(f_{w}\left(\boldsymbol{x}^{(i)}\right) \neq y^{(i)}\right) \ \boldsymbol{w} & \left(f_{w}\left(\boldsymbol{x}^{(i)}\right)=y^{(i)}\right)\end{cases} $$

感知机的缺点是什么？最大的缺点就是它只能解决线性可分的问题。

其中书里提到的感知机太简单了，没有损失函数。也不需要梯度下降。网络查到的感知机是有目标函数，可以梯度下降的。等后面深入了解再补补

3.2 逻辑回归

为什么明明是分类问题，名字还起一个回归呢？那是因为实际是通过得到预测概率值结合 cutoff 来判断这个样本是正还是负样本的。

数据标签：和感知机的标签不同，标签为 0 和 1。：

设计的函数主要是这样子的

$$ f_{\theta}(\boldsymbol{x})=\frac{1}{1+\exp \left(-\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x}\right)} =P(y=1 \mid x) $$

$$ y= \begin{cases}1 & \left(\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x} \geqslant 0\right) \ 0 & \left(\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{x}<0\right)\end{cases} $$

解释下，使用 logistic 函数来产生这样一个 0 到 1 的概率值，利用了 logistic 函数输入值大于 0 时，其值位于 0.5 到 1 之间，小于 0 时，其值位于 0 到 1 之间；

而 $\theta^Tx$ 其实就是分类的线（超平面），我们把它叫做决策边界，$\theta^Tx$ >0 或 <0 说明点在这个边界的一侧或另一侧以进行分类。

目标函数改为似然函数：

$$ \log L(\boldsymbol{\theta})=\log \prod_{i=1}^{n} P\left(y^{(i)}=1 \mid \boldsymbol{x}^{(i)}\right)^{y^{(i)}} P\left(y^{(i)}=0 \mid \boldsymbol{x}^{(i)}\right)^{1-y^{(i)}} $$

别看这样，其实梯度下降依然还是这个公式：

$$ \theta_{j}:=\theta_{j}-\eta \sum_{i=1}^{n}\left(f_{\theta}\left(\boldsymbol{x}^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} \\ f_{\theta}(x)=P(y=1 \mid x) $$

解释下似然函数，书里有这样一句话“似然的意思是最近似的，我们可以认为似然函数 $L(\theta)$ 中，使其值最大的参数 $\theta$ 能够最近似地说明训练数据”，为什么这样说呢？这个似然函数的意思是让 y=1 的样本，判断为 1 的概率最大，让 y=0 的样本，判断为 0 的概率最大，不就是最符合实际情况嘛? 于是目标就是找到一个 $\theta$ ，让这个似然函数的值最大，这时这个 $\theta$ 最能模拟实际情况。

第 4 章 评估——评估已建立的模型

将检查在第 2 章和第 3 章中考虑的模型的精度。我们将学习如何对模型进行评估，以及用于评估的指标有哪些。内容包括

• 交叉验证：把数据分为训练数据和测试数据，使用训练数据训练模型，使用测试数据评估模型。这种方法就叫做交叉验证。
  • 交叉验证最有名的就是 K 折交叉验证，一次留一份留下来做测试，其他分拿去训练，然后循环 k 次，取评估来评估模型。
• 评估模型需要定量描述，如何定量描述预测结果呢？
  • 回归问题的模型性能，可以用均方误差 MSE，误差越小，精度越高
    • 公式：$\frac{1}{n} \sum_{i=1}^{n}\left(y^{(i)}-f_{\theta}\left(\boldsymbol{x}^{(i)}\right)\right)^{2}$
  • 分类问题的模型性能：Accuracy 可以用来评估数据比较平衡的数据集，对于不平衡的情况，可以使用 F1-score（综合考虑 Precision 和 Recall），我之前还了解到 ROC 曲线也可以应对正负样本不均的情况来评估模型性能。 公式： $$ \begin{aligned} \text { Precision } &=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FN}} \ \text { Recall } &=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}} \ \text { F1-score } &=\frac{2 \cdot \text { Precision } \cdot \text { Recall }}{\text { Precision }+\text { Recall }} \end{aligned} $$
• 避免过拟合 overfitting：手段包括增加全部训练数据的数量、使用简单的模型、正则化。重点介绍正则化
  • 正则化：是为了防止模型过拟合加的惩罚，可以防止参数变得过大，有助于参数接近较小的值：尽量往 0 靠（L2 正则化），或者干脆让某些参数为 0（L1 正则化）
  • L2 正则化：$R(\boldsymbol{\theta})=\frac{\lambda}{2} \sum_{j=1}^{m} \theta_{j}^{2}$
  • L1 正则化：$R(\boldsymbol{\theta})=\lambda \sum_{i=1}^{m}\left|\theta_{i}\right|$
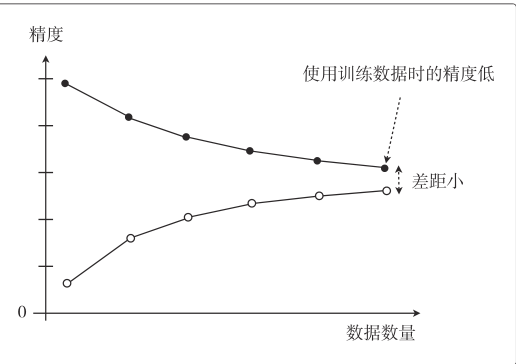
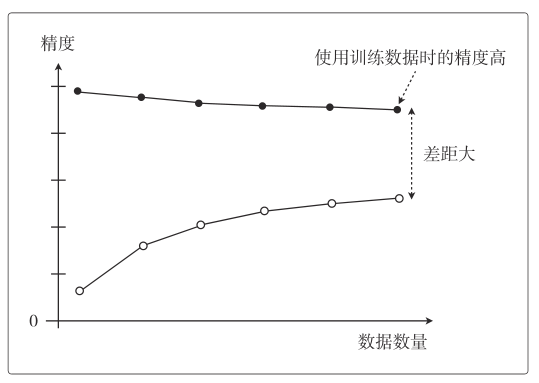
• 学习曲线：通过学习曲线可以判断模型是过拟合 overfitting 还是欠拟合 underfitting
  • 欠拟合 underfitting 的学习曲线：对于训练数据来说，如果模型过于简单，数据量小时可能误差还好，那么随着训练数据量的增加，误差也会一点点变大，精度会一点点下降；对于测试数据来说，随着训练数据量的增加，模型的预测能力会有所提高，但是可能就一直达不到理想的值。是一种即使增加数据的数量，无论是使用训练数据还是测试数据，精度也都会很差的状态。其图形就是这样
    
  • 过拟合 overfitting 的学习曲线：对于训练数据来说，由于过于拟合，模型太复杂，导致精度一直保持很高的水准；然而换了测试数据，就会发现训练数据和测试数据的精度差别很大

第 5 章 实现——使用 Python 编程

根据从第 2 章到第 4 章学到的内容，使用 Python 进行编程。读了这一章

以后，我们就能知道如何把前面用表达式思考的内容编写为代码了

我个人实现的代码见：Achuan-2/math_in_machine_learning

接下来的计划

书：我下本书打算看《Python 神经网络编程》和《深度学习的数学》。

视频课程：

• 目前在看推荐 Ele 实验室的小白也能听懂的人工智能原理，前几课非常搭这本书，我一边看书一边听课非常有收获！课后面讲的就是神经网络了。
• 这个帖子推荐的视频可以参考下？