C data structure A data structure in C is a method of arranging and conserving data in a computer so that it may be quickly accessed and altered.
Classified into two types:
- Linear Data Structures
- Non- Linear Data Structures
A linear data structure in C programming is one where the data pieces are ordered sequentially or linearly. Arrays, linked lists, stacks, and queues are a few examples of linear data structures used in C.
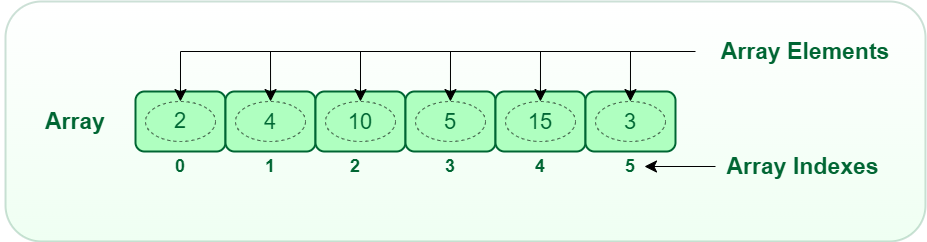
In C, arrays are used to store a predetermined number of identically typed elements.
- Stores a fixed number of elements of the same data type
- Allows random access to elements using index
- Can be used to represent matrices and other mathematical structures
Advantages:
- Simple and easy to use
- Provides fast access to elements using index
- Can be used to implement various algorithms, including sorting and searching algorithms
Disadvantages:
- Fixed size, which can be inefficient if the size of the data set is unknown or dynamic
- Insertion and deletion of elements can be expensive if the array is large
Here is an example of an array that stores 5 integers:
Example Array Code:
#include <stdio.h>
#define SIZE 5
int main() {
int arr[SIZE] = {2, 4, 6, 8, 10};
int i;
for (i = 0; i < SIZE; i++) {
printf("%d ", arr[i]);
}
return 0;
}Output:
2 4 6 8 10
Linked lists in C are used to store a collection of elements in a dynamic way. Linked lists are useful for implementing dynamic data structures that can be easily modified.
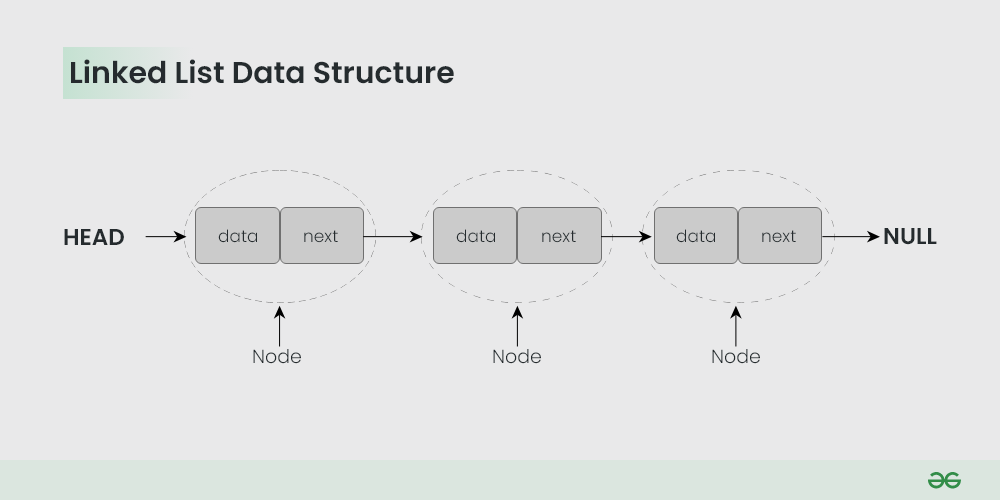
- Dynamic data structure that can grow or shrink as needed
- Provides fast insertion and deletion of elements
- Can be easily traversed using pointers
Advantages:
- Provides efficient memory management
- Allows you to create dynamic data structures that can be easily modified
- Provides fast insertion and deletion of elements
Disadvantages:
- Random access to elements is inefficient
- Can be memory-intensive if used to represent large data sets
Here is an example of a linked list that stores integers.
Example Linked List Code:
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node *next;
};
void printList(struct Node *node) {
while (node != NULL) {
printf("%d ", node->data);
node = node->next;
}
}
int main() {
struct Node* head = NULL;
struct Node* second = NULL;
struct Node* third = NULL;
head = (struct Node*)malloc(sizeof(struct Node));
second = (struct Node*)malloc(sizeof(struct Node));
third = (struct Node*)malloc(sizeof(struct Node));
head->data = 1;
head->next = second;
second->data = 2;
second->next = third;
third->data = 3;
third->next = NULL;
printList(head);
return 0;
} Output:
1 2 3
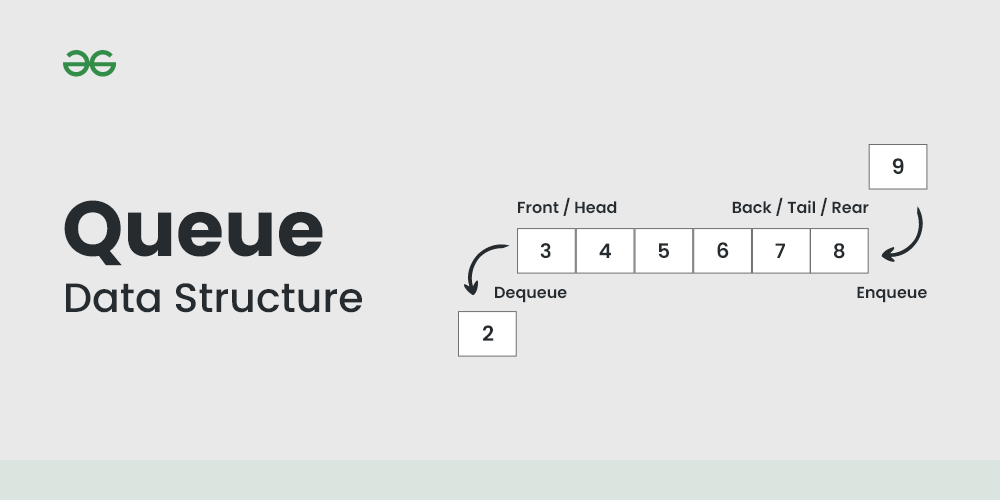
Queues in C are used to store a collection of elements in a first-in, first-out (FIFO) order. For implementing algorithms that need a processing order, queues are helpful.
Characteristics:
- Stores a collection of elements in a first-in, first-out (FIFO) order
- Can be used to implement a wide range of algorithms and data structures
- Provides efficient memory management
Advantages:
- Provides a simple and efficient way to implement algorithms that require a FIFO order
- Can be easily implemented using an array or a linked list
- Provides fast access to the first element in the queue
Disadvantages:
- Random access to elements is inefficient
- Can be inefficient if used to implement algorithms that require random access to elements
Here is an example of a queue that stores integers:
Example Queues Code:
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 100
// define the structure for the queue
struct queue {
int items[MAX_SIZE];
int front;
int rear;
};
// function to create an empty queue
struct queue* createQueue() {
struct queue* q = malloc(sizeof(struct queue));
q->front = -1;
q->rear = -1;
return q;
}
// function to check if the queue is empty
int isEmpty(struct queue* q) {
if (q->rear == -1)
return 1;
else
return 0;
}
// function to add an element to the queue
void enqueue(struct queue* q, int value) {
if (q->rear == MAX_SIZE - 1)
printf("Queue is full!");
else {
if (q->front == -1)
q->front = 0;
q->rear++;
q->items[q->rear] = value;
}
}
// function to remove an element from the queue
int dequeue(struct queue* q) {
int item;
if (isEmpty(q)) {
printf("Queue is empty");
item = -1;
} else {
item = q->items[q->front];
q->front++;
if (q->front > q->rear) {
q->front = q->rear = -1;
}
}
return item;
}
int main() {
struct queue* q = createQueue();
enqueue(q, 1);
enqueue(q, 2);
enqueue(q, 3);
printf("Dequeued item: %d\n", dequeue(q));
printf("Dequeued item: %d\n", dequeue(q));
printf("Dequeued item: %d\n", dequeue(q));
return 0;
} Output:
Dequeued item: 1
Dequeued item: 2
Dequeued item: 3
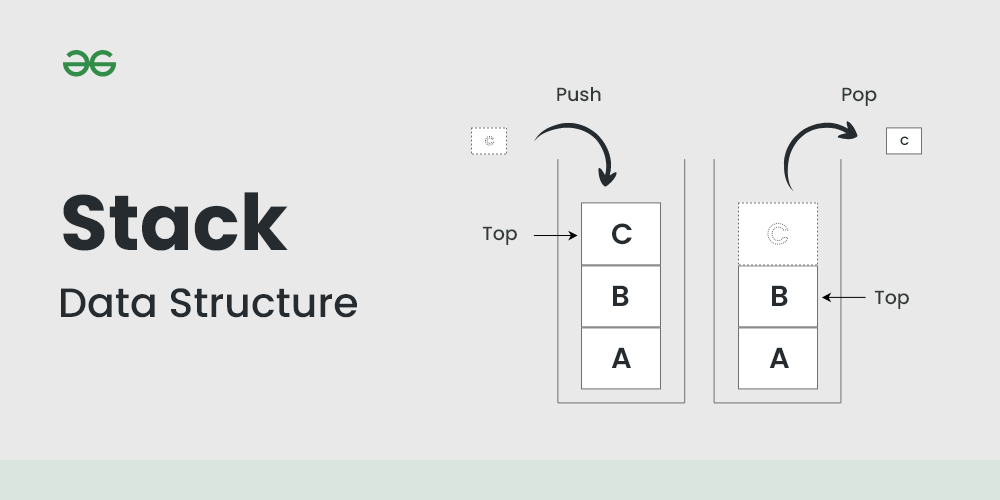
Last-in, first-out (LIFO) order is used to store a group of elements in stacks in the C programming language. For implementing algorithms that need a hierarchical ordering, stacks are helpful.
- Stores a collection of elements in a last-in, first-out (LIFO) order
- Can be used to implement a wide range of algorithms and data structures
- Provides efficient memory management
Advantages:
- Provides a simple and efficient way to implement algorithms that require a LIFO order
- Can be easily implemented using an array or a linked list
- Provides fast access to the top element in the stack
Disadvantages:
- Random access to elements is inefficient
- Can be inefficient if used to implement algorithms that require random access to elements
Here is an example of a stack that stores integers:
Example Stack Code:
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 100
// define the structure for the stack
struct stack {
int items[MAX_SIZE];
int top;
};
// function to create an empty stack
struct stack* createStack() {
struct stack* s = malloc(sizeof(struct stack));
s->top = -1;
return s;
}
// function to check if the stack is empty
int isEmpty(struct stack* s) {
if (s->top == -1)
return 1;
else
return 0;
}
// function to check if the stack is full
int isFull(struct stack* s) {
if (s->top == MAX_SIZE - 1)
return 1;
else
return 0;
}
// function to add an element to the stack
void push(struct stack* s, int value) {
if (isFull(s))
printf("Stack is full!");
else {
s->top++;
s->items[s->top] = value;
}
}
// function to remove an element from the stack
int pop(struct stack* s) {
int item;
if (isEmpty(s)) {
printf("Stack is empty");
item = -1;
} else {
item = s->items[s->top];
s->top--;
}
return item;
}
int main() {
struct stack* s = createStack();
push(s, 1);
push(s, 2);
push(s, 3);
printf("Popped item: %d\n", pop(s));
printf("Popped item: %d\n", pop(s));
printf("Popped item: %d\n", pop(s));
return 0;
} Output:
Popped item: 3
Popped item: 2
Popped item: 1
Non-linear data structures are those where the elements are not organized in a linear or sequential manner, unlike arrays and linked lists. Instead, the elements may be arranged in a hierarchical, tree-like, or graph-like structure.
Non-linear data structures include, for instance:
A tree is a hierarchical data structure in which every node has at least one child and at least one parent. The bottom nodes are referred to as leaves, and the uppermost node is known as the root. Uncommon tree data structures include binary trees.
- Characteristics: Trees are hierarchical data structures made up of nodes, each of which has a parent and zero to many offspring. In trees, leaf nodes and roots both lack parents and have no offspring. Binary trees (each node has a maximum of two children) and n-ary trees (each node has a maximum of n children) are two types of trees that can be categorised based on the maximum number of children that each node can have.
- Advantages: Trees are useful for representing hierarchical relationships between data, such as file systems, organization charts, and family trees. Additionally, they are employed in search algorithms with logarithmic time complexity for searching, introducing, and removing elements, like binary search trees.
- Disadvantages: Trees can have poor worst-case performance if they become unbalanced, meaning that one branch of the tree is much longer than the others. This can result in linear time complexity for search, insertion, and deletion operations.
Here is an example of tree:
Example Tree Code:
// Tree traversal in C
#include <stdio.h>
#include <stdlib.h>
struct node {
int item;
struct node* left;
struct node* right;
};
// Inorder traversal
void inorderTraversal(struct node* root) {
if (root == NULL) return;
inorderTraversal(root->left);
printf("%d ->", root->item);
inorderTraversal(root->right);
}
// Preorder traversal
void preorderTraversal(struct node* root) {
if (root == NULL) return;
printf("%d ->", root->item);
preorderTraversal(root->left);
preorderTraversal(root->right);
}
// Postorder traversal
void postorderTraversal(struct node* root) {
if (root == NULL) return;
postorderTraversal(root->left);
postorderTraversal(root->right);
printf("%d ->", root->item);
}
// Create a new Node
struct node* createNode(value) {
struct node* newNode = malloc(sizeof(struct node));
newNode->item = value;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
// Insert on the left of the node
struct node* insertLeft(struct node* root, int value) {
root->left = createNode(value);
return root->left;
}
// Insert on the right of the node
struct node* insertRight(struct node* root, int value) {
root->right = createNode(value);
return root->right;
}
int main() {
struct node* root = createNode(1);
insertLeft(root, 2);
insertRight(root, 3);
insertLeft(root->left, 4);
printf("Inorder traversal \n");
inorderTraversal(root);
printf("\nPreorder traversal \n");
preorderTraversal(root);
printf("\nPostorder traversal \n");
postorderTraversal(root);
} Output:
Inorder traversal
4 ->2 ->1 ->3 ->
Preorder traversal
1 ->2 ->4 ->3 ->
Postorder traversal
4 ->2 ->3 ->1 ->
A graph is made up of nodes, or vertices, and the connecting edges. We know that graphs can be cyclic or acyclic, directed or undirected and also weighted or unweighted.
- Characteristics: Graphs are nothing but the collections of the nodes (also known as the vertices) connected by the edges. Edges can include weights to represent the cost or distance between vertices and can be either directed or undirected. Graphs can be classified based on the presence of cycles, such as acyclic graphs (no cycles) and cyclic graphs (one or more cycles).
- Advantages: Graphs are useful for representing complex relationships between data, such as social networks, transportation networks, and computer networks. They are also used in algorithms for shortest path, minimum spanning tree, and network flow problems.
- Disadvantages: Graphs can be difficult to manipulate and analyse because of their complexity. Algorithms for graph problems can have high time and space complexity, especially for large graphs.
Here is an example of a graph:
Example Graph Code:
#include <stdio.h>
#include <stdlib.h>
// We are defining the maximum number of vertices in the graph
#define N 6
// It is a data structure to store a graph object
struct Graph
{
// An adjacency list can be represented by an array of pointers to Nodes
struct Node* head[N];
};
// An adjacency list for the graph's nodes is kept in a data structure.
struct Node
{
int dest;
struct Node* next;
};
// An edge-storing data structure for graphs
struct Edge {
int src, dest;
};
// Function to create an adjacency list from specified edges
struct Graph* createGraph(struct Edge edges[], int n)
{
// allocate storage for the graph data structure
struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));
// initialize head pointer for all vertices
for (int i = 0; i < N; i++) {
graph->head[i] = NULL;
}
// add edges to the directed graph one by one
for (int i = 0; i < n; i++)
{
// get the source and destination vertex
int src = edges[i].src;
int dest = edges[i].dest;
// allocate a new node of adjacency list from src to dest
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->dest = dest;
// point new node to the current head
newNode->next = graph->head[src];
// point head pointer to the new node
graph->head[src] = newNode;
}
return graph;
}
// Function to print adjacency list representation of a graph
void printGraph(struct Graph* graph)
{
for (int i = 0; i < N; i++)
{
// print current vertex and all its neighbors
struct Node* ptr = graph->head[i];
while (ptr != NULL)
{
printf("(%d ?> %d)\t", i, ptr->dest);
ptr = ptr->next;
}
printf("\n");
}
}
// Directed graph implementation in C
int main(void)
{
// input array containing edges of the graph (as per the above diagram)
// (x, y) pair in the array represents an edge from x to y
struct Edge edges[] =
{
{0, 1}, {1, 2}, {2, 0}, {2, 1}, {3, 2}, {4, 5}, {5, 4}
};
// calculate the total number of edges
int n = sizeof(edges)/sizeof(edges[0]);
// construct a graph from the given edges
struct Graph *graph = createGraph(edges, n);
// Function to print adjacency list representation of a graph
printGraph(graph);
return 0;
} Output:
(0 ?> 1)
(1 ?> 2)
(2 ?> 1) (2 ?> 0)
(3 ?> 2)
(4 ?> 5)
(5 ?> 4)
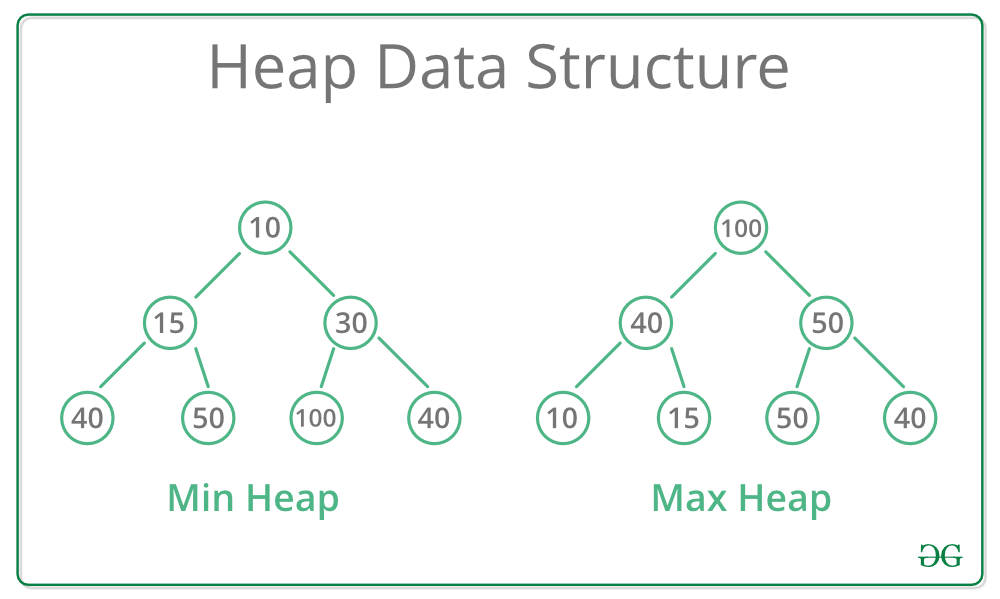
A heap is a specialized tree-based data structure that satisfies the heap property. In a min-heap, the parent node is always smaller than its children, and in a max-heap, the parent node is always larger than its children.
- Characteristics: Heaps are tree-based data structures that satisfy the heap property, which is that the value of each parent node is greater than or equal to the value of its children (for a max heap) or less than or equal to the value of its children (for a min heap). Heaps are often implemented as binary trees, with each node representing an element of the heap.
- Advantages: Heaps are useful for implementing priority queues, where elements are removed from the queue in order of priority (i.e., the highest or lowest value). They are also used in sorting algorithms, such as heapsort, which has a time complexity of O(n log n).
- Disadvantages: Heaps can have poor worst-case performance for inserting elements, especially if the heap becomes unbalanced. Also, because heaps are typically implemented as binary trees, they can have wasted space if the number of elements in the heap is not a power of two.
Here is an example of heap:
Example Heap Code:
// Max-Heap data structure in C
#include <stdio.h>
int size = 0;
void swap(int *a, int *b)
{
int temp = *b;
*b = *a;
*a = temp;
}
void heapify(int array[], int size, int i)
{
if (size == 1)
{
printf("Single element in the heap");
}
else
{
int largest = i;
int l = 2 * i + 1;
int r = 2 * i + 2;
if (l < size && array[l] > array[largest])
largest = l;
if (r < size && array[r] > array[largest])
largest = r;
if (largest != i)
{
swap(&array[i], &array[largest]);
heapify(array, size, largest);
}
}
}
void insert(int array[], int newNum)
{
if (size == 0)
{
array[0] = newNum;
size += 1;
}
else
{
array[size] = newNum;
size += 1;
for (int i = size / 2 - 1; i >= 0; i--)
{
heapify(array, size, i);
}
}
}
void deleteRoot(int array[], int num)
{
int i;
for (i = 0; i < size; i++)
{
if (num == array[i])
break;
}
swap(&array[i], &array[size - 1]);
size -= 1;
for (int i = size / 2 - 1; i >= 0; i--)
{
heapify(array, size, i);
}
}
void printArray(int array[], int size)
{
for (int i = 0; i < size; ++i)
printf("%d ", array[i]);
printf("\n");
}
int main()
{
int array[10];
insert(array, 3);
insert(array, 4);
insert(array, 9);
insert(array, 5);
insert(array, 2);
printf("Max-Heap array: ");
printArray(array, size);
deleteRoot(array, 4);
printf("After deleting an element: ");
printArray(array, size);
} Output:
Max-Heap array: 9 5 4 3 2
After deleting an element: 9 5 2 3
These are just a few examples of non-linear data structures, and there are many more that are used in various applications.
In conclusion, linear and non-linear data structures are both important in computer science and can be implemented using the C programming language.
Linear data structures, such as arrays, linked lists, and stacks, have a simple linear organization and are useful for storing data in a sequential manner. They have the advantage of fast access to elements in the middle of the structure, but can have slower performance for inserting or deleting elements in the middle of the structure.
Non-linear data structures, such as trees, graphs, and heaps, have a more complex organization and are useful for storing data with hierarchical or interconnected relationships. They have the advantage of efficient searching, insertion, and deletion operations, but can have worse performance for access to elements in the middle of the structure.
The choice of data structure depends on the specific requirements of the problem being solved. Linear data structures are more suitable for problems where data needs to be accessed sequentially or where the size of the data is known in advance. Non-linear data structures are more suitable for problems where the data has complex relationships or where efficient search, insertion, and deletion operations are required.
In C programming, both linear and non-linear data structures can be implemented using arrays, pointers, and structures. There are also many libraries and frameworks available that provide implementations of common data structures, such as the Standard Template Library (STL) in C++. Understanding the characteristics, advantages, and disadvantages of different data structures is an important skill for computer scientists and software developers.