6DOF robot kinematics in JavaScript.
npm install kinematics --saveconst Kinematics = require('kinematics').default
const geometry = [
[1, 1, 0], // V0: 1x 1y
[0, 10, 0], // V1: 10y
[5, 0, 0], // V2: 5x
[3, 0, 0], // V3: 3x
[0, -3, 0], // V4: -3y
]
const RobotKin = new Kinematics(geometry)
let angles = [1.57, 1.2, 0, 0.3, 2.2, 1.1]
const pose = RobotKin.forward(...angles)[5]
angles = RobotKin.inverse(...pose)The geometry array consists of 5 entries describing the links V0-V5. Each Vn is a tuple of 3 coordinates from Jn to Jn+1. One constraint: The y,z of V3 and x,z of V4 must be 0 for the kinematics to work.
forward
RobotKin.forward(R0, R1, R2, R3, R4, R5)returns
[
[ 0, 0, 0 ], //J0
[ 0.5, 1, -0.8 ], //J1
[ -0.2, -8.8, 0.3 ], //J2
[ 1.8, -5.6, -2.8 ], //J3
[ 3.0, -3.6, -4.7 ], //J4
[ 4.7, -1.3, -5.5, 1, 6, -2.8 ] //J5 + TCP Euler angles
]
inverse
X,Y,Z coordinates, A,B,C Euler angles in order 'abc'.
RobotKin.inverse(X, Y, Z, A, B, C)returns
[ 2, 1.6, 2.1, -3.5, 1, -1.5 ] //array of angles
[ 1, 2.3, 3.1, NaN, NaN, NaN ] //NaN for out of reach angles
kinematics.js assumes a robot with a series of joints. Some robots may have different kinematics. The depicted robot has a hinge at J1 and R1/R2 are at the same kinematic position. Therefore moving R1 also changes the angle at J2. To account for that, R2 has to move the same amount.
Using that information, you can use kinematics.js to calculate the initial angles and correct them according to your kinematics.
let angles = RobotKin.inverse(...pose)
angles[2] += angles[1]
//set angles, do stuff 🤖- robot configuration
- comply with DH for TCP orientation?
- more kinematic chains
See the kinematics in action: http://robot.glumb.de (Use Chrome or FF due to ES6 features)
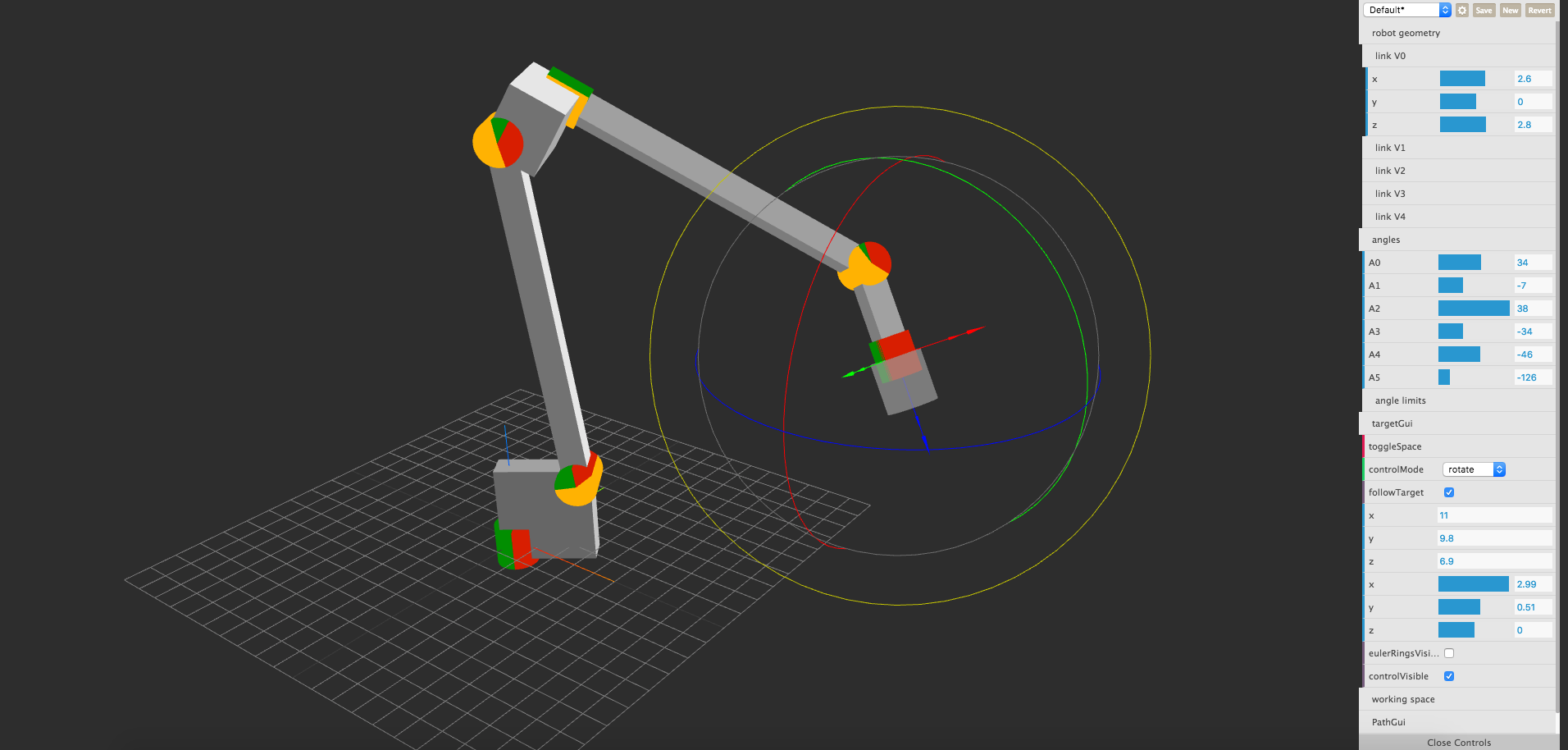 The gui is available in this repo:https://github.com/glumb/robot-gui
The gui is available in this repo:https://github.com/glumb/robot-gui






