给你一棵 树(即一个连通、无向、无环图),根节点是节点 0 ,这棵树由编号从 0 到 n - 1 的 n 个节点组成。用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树,其中 parent[i] 是节点 i 的父节点,由于节点 0 是根节点,所以 parent[0] == -1 。
另给你一个字符串 s ,长度也是 n ,其中 s[i] 表示分配给节点 i 的字符。
请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径 ,并返回该路径的长度。
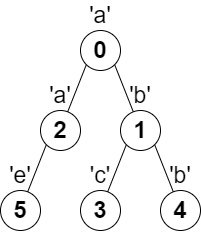
示例 1:
输入:parent = [-1,0,0,1,1,2], s = "abacbe" 输出:3 解释:任意一对相邻节点字符都不同的最长路径是:0 -> 1 -> 3 。该路径的长度是 3 ,所以返回 3 。 可以证明不存在满足上述条件且比 3 更长的路径。
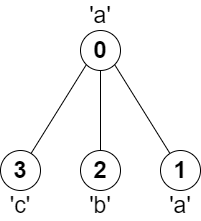
示例 2:
输入:parent = [-1,0,0,0], s = "aabc" 输出:3 解释:任意一对相邻节点字符都不同的最长路径是:2 -> 0 -> 3 。该路径的长度为 3 ,所以返回 3 。
提示:
n == parent.length == s.length1 <= n <= 105- 对所有
i >= 1,0 <= parent[i] <= n - 1均成立 parent[0] == -1parent表示一棵有效的树s仅由小写英文字母组成
function longestPath(parent: number[], s: string): number {
const n = parent.length;
let graph = Array.from({ length: n }, v => []);
for (let i = 1; i < n; i++) {
graph[parent[i]].push(i);
}
let ans = 0;
function dfs(x: number): number {
let maxLen = 0;
for (let y of graph[x]) {
let len = dfs(y) + 1;
if (s.charAt(x) !== s.charAt(y)) {
ans = Math.max(maxLen + len, ans);
maxLen = Math.max(len, maxLen);
}
}
return maxLen;
}
dfs(0);
return ans + 1;
}