|
2 | 2 |
|
3 | 3 | ## 题目描述 |
4 | 4 |
|
5 | | -我们从二叉树的根节点 `root` 开始进行深度优先搜索。 |
| 5 | +给定一个含有 **n** 个正整数的数组和一个正整数 **s** ,找出该数组中满足其和 **≥ s** 的长度最小的连续子数组,并返回其长度。如果不存在符合条件的连续子数组,返回 0。 |
6 | 6 |
|
7 | | -在遍历中的每个节点处,我们输出 `D` 条短划线(其中 `D` 是该节点的深度),然后输出该节点的值。(_如果节点的深度为 `D`,则其直接子节点的深度为 `D + 1`。根节点的深度为 `0`)。_ |
8 | | - |
9 | | -如果节点只有一个子节点,那么保证该子节点为左子节点。 |
10 | | - |
11 | | -给出遍历输出 `S`,还原树并返回其根节点 `root`。 |
12 | | - |
13 | | -**示例 1:** |
14 | | - |
15 | | -**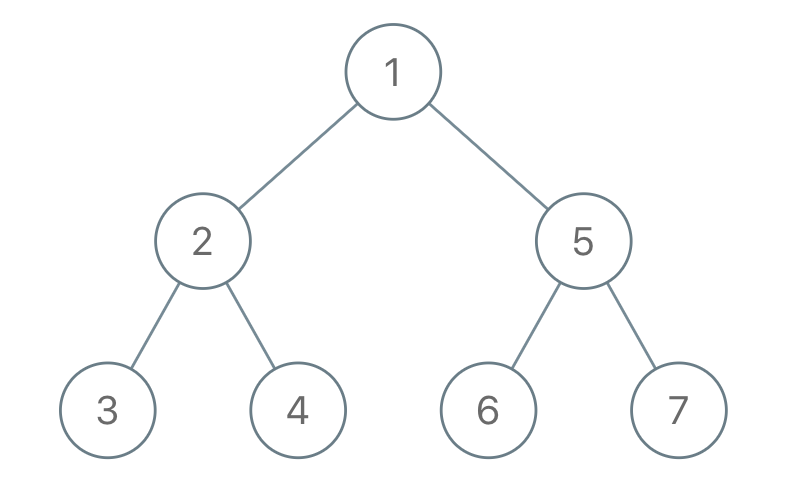** |
| 7 | +**示例:** |
16 | 8 |
|
17 | 9 | ``` |
18 | | -输入:"1-2--3--4-5--6--7" |
19 | | -输出:[1,2,5,3,4,6,7] |
| 10 | +输入:s = 7, nums = [2,3,1,2,4,3] |
| 11 | +输出:2 |
| 12 | +解释:子数组 [4,3] 是该条件下的长度最小的连续子数组。 |
20 | 13 | ``` |
21 | 14 |
|
22 | | -**示例 2:** |
| 15 | +**进阶:** |
23 | 16 |
|
24 | | -**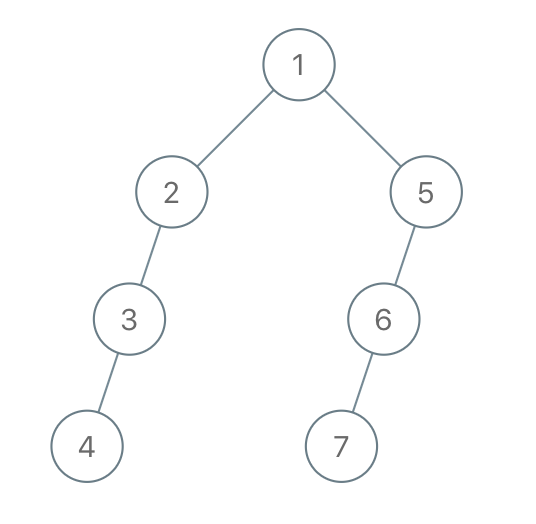** |
| 17 | +* 如果你已经完成了 _O_(_n_) 时间复杂度的解法, 请尝试 _O_(_n_ log _n_) 时间复杂度的解法。 |
25 | 18 |
|
26 | | -``` |
27 | | -输入:"1-2--3---4-5--6---7" |
28 | | -输出:[1,2,5,3,null,6,null,4,null,7] |
29 | | -``` |
| 19 | +**标签:** 数组、双指针、二分查找 |
30 | 20 |
|
31 | | -**示例 3:** |
32 | 21 |
|
33 | | -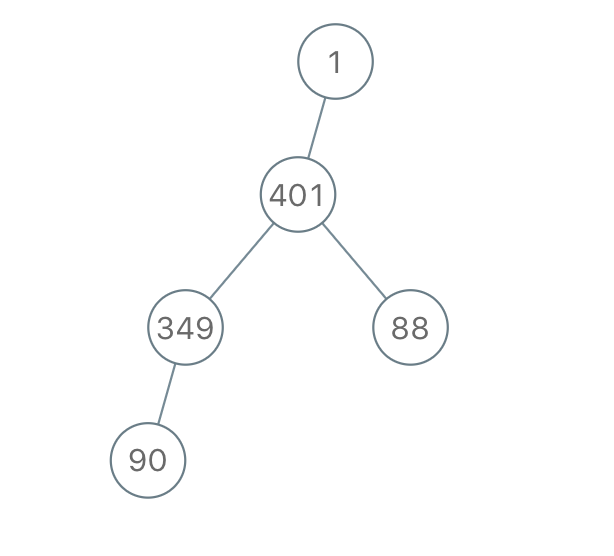 |
| 22 | +## 思路 0 |
34 | 23 |
|
35 | | -``` |
36 | | -输入:"1-401--349---90--88" |
37 | | -输出:[1,401,null,349,88,90] |
| 24 | +直接暴力法,两重 for 循环,记录最小长度即可,代码很简单,如下所示: |
| 25 | + |
| 26 | + |
| 27 | +```java |
| 28 | +class Solution { |
| 29 | + public int minSubArrayLen(int s, int[] nums) { |
| 30 | + int ans = Integer.MAX_VALUE; |
| 31 | + for (int i = 0; i < nums.length; i++) { |
| 32 | + int sum = nums[i]; |
| 33 | + if (sum >= s) { |
| 34 | + return 1; |
| 35 | + } |
| 36 | + for (int j = i + 1; j < nums.length; j++) { |
| 37 | + sum += nums[j]; |
| 38 | + if (sum >= s) { |
| 39 | + ans = Math.min(ans, j - i + 1); |
| 40 | + break; |
| 41 | + } |
| 42 | + } |
| 43 | + } |
| 44 | + return ans == Integer.MAX_VALUE ? 0 : ans; |
| 45 | + } |
| 46 | +} |
38 | 47 | ``` |
39 | 48 |
|
40 | | -**提示:** |
| 49 | +## 思路 1 |
41 | 50 |
|
42 | | -* 原始树中的节点数介于 `1` 和 `1000` 之间。 |
43 | | -* 每个节点的值介于 `1` 和 `10 ^ 9` 之间。 |
| 51 | +对上面进行优化,我们通过首位两个指针来模拟滑动窗口,如果加起来值小于 s,则向右扩大窗口直至不小于 s,然后固定窗口右侧来向左缩小窗口,同时更新符合条件的最小窗口长度即可,代码如下所示: |
44 | 52 |
|
45 | | -**标签:** 树、深度优先搜索 |
| 53 | +```java |
| 54 | +class Solution { |
| 55 | + public int minSubArrayLen(int s, int[] nums) { |
| 56 | + int left = 0, right = 0, sum = 0, ans = Integer.MAX_VALUE; |
| 57 | + while (right < nums.length) { |
| 58 | + sum += nums[right++]; // 向右扩大窗口 |
| 59 | + while (sum >= s) { // 如果不小于 s,则收缩窗口左边界 |
| 60 | + ans = Math.min(ans, right - left);// 更新结果 |
| 61 | + sum -= nums[left++]; // 向左缩小窗口 |
| 62 | + } |
| 63 | + } |
| 64 | + return ans == Integer.MAX_VALUE ? 0 : ans; |
| 65 | + } |
| 66 | +} |
| 67 | +``` |
46 | 68 |
|
| 69 | +## 思路 2 |
47 | 70 |
|
48 | | -## 思路 |
| 71 | +进阶中说了,尝试使用 O(nlogn) 时间复杂度的解法,由于数组都是正整数构成,所以前缀和一定是递增的,想到的应该就是用二分查找了,可以用 sums 数组来存储 nums 数组的前缀和,sums[i] 代表 nums[0] 到 nums[i - 1] 总和,然后遍历 sums 数组,对 sums[i] + s 进行二分查找然后不断更新结果即可,具体代码如下所示: |
49 | 72 |
|
50 | | -直接暴力两层 for 循环肯定过不了关,我们把公式变化为 `(A[i] + i) + (A[j] - j)`,看到此应该就可以想到在每次遍历 `j` 时,只需要知道 `max(A[i] + i)` 即可。 |
51 | 73 |
|
52 | 74 | ```java |
53 | 75 | class Solution { |
54 | | - |
55 | | - public int maxScoreSightseeingPair(int[] A) { |
56 | | - int ans = 0, cur = A[0] + 0; |
57 | | - for (int j = 1; j < A.length; j++) { |
58 | | - ans = Math.max(ans, cur + A[j] - j); // 计算当前最大得分 |
59 | | - cur = Math.max(cur, A[j] + j); // 更新最大的 A[i] + i |
| 76 | + public int minSubArrayLen(int s, int[] nums) { |
| 77 | + int ans = Integer.MAX_VALUE; |
| 78 | + int[] sums = new int[nums.length + 1]; |
| 79 | + for (int i = 0; i < nums.length; i++) { |
| 80 | + sums[i + 1] = sums[i] + nums[i]; |
60 | 81 | } |
61 | | - return ans; |
62 | | - } |
63 | | - |
64 | | - public static void main(String[] args) { |
65 | | - Solution solution = new Solution(); |
66 | | - int[] A = new int[]{8, 1, 5, 2, 6}; |
67 | | - System.out.println(solution.maxScoreSightseeingPair(A)); |
| 82 | + for (int i = 0; i < nums.length; i++) { |
| 83 | + int target = s + sums[i]; // 确定要搜索的目标值 |
| 84 | + // Java 二分查找 Arrays.binarySearch 如果找到就会返回该元素的索引; |
| 85 | + // 如果没找到就会返回一个负数,这个负数取反之后再减一就是查找的值应该在数组中的位置; |
| 86 | + // 例如 [-1, 0, 1, 5] 中二分查找 2,其返回值就是 -4,其 -(-4) - 1 = 3,所以 2 这个元素插入到数组的索引就是 3 |
| 87 | + int bound = Arrays.binarySearch(sums, target); |
| 88 | + if (bound < 0) { |
| 89 | + bound = -bound - 1; |
| 90 | + } |
| 91 | + if (bound < sums.length) { // 当 bound 确定插入点不在 sums 数组的最后面时,说明不小于 target 的值了 |
| 92 | + ans = Math.min(ans, bound - i); |
| 93 | + } |
| 94 | + } |
| 95 | + return ans == Integer.MAX_VALUE ? 0 : ans; |
68 | 96 | } |
69 | 97 | } |
70 | | - |
71 | 98 | ``` |
72 | 99 |
|
73 | | - |
74 | 100 | ## 结语 |
75 | 101 |
|
76 | 102 | 如果你同我一样热爱数据结构、算法、LeetCode,可以关注我 GitHub 上的 LeetCode 题解:[awesome-java-leetcode][ajl] |
77 | 103 |
|
78 | 104 |
|
79 | 105 |
|
80 | | -[title]: https://leetcode-cn.com/problems/recover-a-tree-from-preorder-traversal |
| 106 | +[title]: https://leetcode-cn.com/problems/minimum-size-subarray-sum |
81 | 107 | [ajl]: https://github.com/Blankj/awesome-java-leetcode |
0 commit comments