|
| 1 | +# 2392. Build a Matrix With Conditions |
| 2 | + |
| 3 | +- Difficulty: Hard. |
| 4 | +- Related Topics: Array, Graph, Topological Sort, Matrix. |
| 5 | +- Similar Questions: Course Schedule, Course Schedule II, Find Eventual Safe States, Loud and Rich. |
| 6 | + |
| 7 | +## Problem |
| 8 | + |
| 9 | +You are given a **positive** integer `k`. You are also given: |
| 10 | + |
| 11 | + |
| 12 | + |
| 13 | +- a 2D integer array `rowConditions` of size `n` where `rowConditions[i] = [abovei, belowi]`, and |
| 14 | + |
| 15 | +- a 2D integer array `colConditions` of size `m` where `colConditions[i] = [lefti, righti]`. |
| 16 | + |
| 17 | + |
| 18 | +The two arrays contain integers from `1` to `k`. |
| 19 | + |
| 20 | +You have to build a `k x k` matrix that contains each of the numbers from `1` to `k` **exactly once**. The remaining cells should have the value `0`. |
| 21 | + |
| 22 | +The matrix should also satisfy the following conditions: |
| 23 | + |
| 24 | + |
| 25 | + |
| 26 | +- The number `abovei` should appear in a **row** that is strictly **above** the row at which the number `belowi` appears for all `i` from `0` to `n - 1`. |
| 27 | + |
| 28 | +- The number `lefti` should appear in a **column** that is strictly **left** of the column at which the number `righti` appears for all `i` from `0` to `m - 1`. |
| 29 | + |
| 30 | + |
| 31 | +Return ****any** matrix that satisfies the conditions**. If no answer exists, return an empty matrix. |
| 32 | + |
| 33 | + |
| 34 | +Example 1: |
| 35 | + |
| 36 | +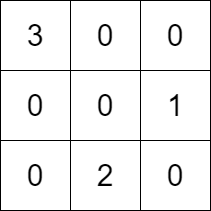 |
| 37 | + |
| 38 | +``` |
| 39 | +Input: k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]] |
| 40 | +Output: [[3,0,0],[0,0,1],[0,2,0]] |
| 41 | +Explanation: The diagram above shows a valid example of a matrix that satisfies all the conditions. |
| 42 | +The row conditions are the following: |
| 43 | +- Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix. |
| 44 | +- Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix. |
| 45 | +The column conditions are the following: |
| 46 | +- Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix. |
| 47 | +- Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix. |
| 48 | +Note that there may be multiple correct answers. |
| 49 | +``` |
| 50 | + |
| 51 | +Example 2: |
| 52 | + |
| 53 | +``` |
| 54 | +Input: k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]] |
| 55 | +Output: [] |
| 56 | +Explanation: From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied. |
| 57 | +No matrix can satisfy all the conditions, so we return the empty matrix. |
| 58 | +``` |
| 59 | + |
| 60 | + |
| 61 | +**Constraints:** |
| 62 | + |
| 63 | + |
| 64 | + |
| 65 | +- `2 <= k <= 400` |
| 66 | + |
| 67 | +- `1 <= rowConditions.length, colConditions.length <= 104` |
| 68 | + |
| 69 | +- `rowConditions[i].length == colConditions[i].length == 2` |
| 70 | + |
| 71 | +- `1 <= abovei, belowi, lefti, righti <= k` |
| 72 | + |
| 73 | +- `abovei != belowi` |
| 74 | + |
| 75 | +- `lefti != righti` |
| 76 | + |
| 77 | + |
| 78 | + |
| 79 | +## Solution |
| 80 | + |
| 81 | +```javascript |
| 82 | +/** |
| 83 | + * @param {number} k |
| 84 | + * @param {number[][]} rowConditions |
| 85 | + * @param {number[][]} colConditions |
| 86 | + * @return {number[][]} |
| 87 | + */ |
| 88 | +var buildMatrix = function(k, rowConditions, colConditions) { |
| 89 | + var rowOrder = topologicalSort(k, rowConditions); |
| 90 | + var colOrder = topologicalSort(k, colConditions); |
| 91 | + if (!rowOrder || !colOrder) return []; |
| 92 | + var colOrderMap = colOrder.reduce((map, n, i) => { |
| 93 | + map[n] = i; |
| 94 | + return map; |
| 95 | + }, {}); |
| 96 | + var matrix = Array(k).fill(0).map(() => Array(k).fill(0)); |
| 97 | + rowOrder.forEach((n, i) => matrix[i][colOrderMap[n]] = n); |
| 98 | + return matrix; |
| 99 | +}; |
| 100 | + |
| 101 | +var topologicalSort = function(k, arr) { |
| 102 | + var beforeMap = Array(k).fill(0); |
| 103 | + var afterMap = Array(k).fill(0).map(() => []); |
| 104 | + for (var i = 0; i < arr.length; i++) { |
| 105 | + beforeMap[arr[i][1] - 1] += 1; |
| 106 | + afterMap[arr[i][0] - 1].push(arr[i][1]); |
| 107 | + } |
| 108 | + var queue = []; |
| 109 | + for (var j = 0; j < k; j++) { |
| 110 | + if (beforeMap[j] === 0) { |
| 111 | + queue.push(j + 1); |
| 112 | + } |
| 113 | + } |
| 114 | + var res = []; |
| 115 | + while (queue.length) { |
| 116 | + var num = queue.shift(); |
| 117 | + afterMap[num - 1].forEach(n => { |
| 118 | + if (--beforeMap[n - 1] === 0) { |
| 119 | + queue.push(n); |
| 120 | + } |
| 121 | + }); |
| 122 | + res.push(num); |
| 123 | + } |
| 124 | + if (res.length === k) { |
| 125 | + return res; |
| 126 | + } |
| 127 | + return null; |
| 128 | +}; |
| 129 | +``` |
| 130 | + |
| 131 | +**Explain:** |
| 132 | + |
| 133 | +nope. |
| 134 | + |
| 135 | +**Complexity:** |
| 136 | + |
| 137 | +* Time complexity : O(k). |
| 138 | +* Space complexity : O(k ^ 2). |
0 commit comments